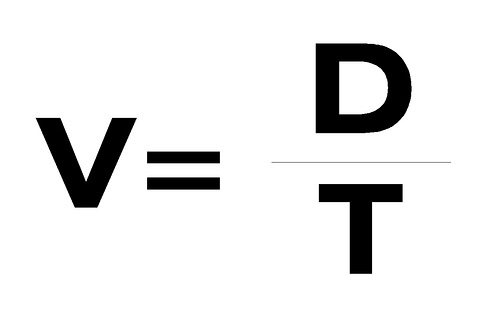Nesta última clase de matemáticas antes do exame aprobeitamos para plantexar o último problema da folla de exercicios, o 37. A continuación móstrovos a súa corección no seguite enlace:
EXERCICIO 37
A segunda parte da clase consistiu nunha pequena introducción das inecuacións, onde para entendelas mellor, a profe Aia nos explicou o porqué do motivo polo cal cambiamos un termo da ecuación de lado, xa que as inecuacións están relacionadas coas ecuacións. Isto é unha inecuación:
xoves, 28 de xaneiro de 2016
mércores, 27 de xaneiro de 2016
Corrección problemas de ecuacións
Nesta clase seguimos corrixindo problemas de ecuacións, xa que a todos nós nos custaba plantexalos e só quedan un par de días para que fose o exame.
Había tres exercicios, dous máis sinxelos, é dicir, de ecuacións con unha incógnita e outro con tres incógnitas.
O de tres incógnitas:
1-Primeiro asignamos as incógnitas.
x - o lado ao que lle vas aumentar 3 cm
y - o outro lado
z - o lado y xa disminuído
2- Unha vez feito isto plantexamos o problema e o resolvemos:
2x+2y = 46 -(dividimos entre 2) - x+y =23 - y = 23-x - y = 23-15 = 8
xy-30 = (x+3) z -(quitamos parénteses) - xy-xz-3z =30
2(x+3)+2z = 46 -(quitamos parénteses - x+z =20 - z = 20-x - z =20-15 = 5
e dividimos entre 2)
3-E por último resolvemos a ecuación 2 substituíndo z e y polo seu valor dando así x = 15
Había tres exercicios, dous máis sinxelos, é dicir, de ecuacións con unha incógnita e outro con tres incógnitas.
O de tres incógnitas:
1-Primeiro asignamos as incógnitas.
x - o lado ao que lle vas aumentar 3 cm
y - o outro lado
z - o lado y xa disminuído
2- Unha vez feito isto plantexamos o problema e o resolvemos:
2x+2y = 46 -(dividimos entre 2) - x+y =23 - y = 23-x - y = 23-15 = 8
xy-30 = (x+3) z -(quitamos parénteses) - xy-xz-3z =30
2(x+3)+2z = 46 -(quitamos parénteses - x+z =20 - z = 20-x - z =20-15 = 5
e dividimos entre 2)
3-E por último resolvemos a ecuación 2 substituíndo z e y polo seu valor dando así x = 15
martes, 26 de xaneiro de 2016
Plantexamento dos problemas.
Luns 25/01/2016
Problemas problemas e máis problemas.
Pois a primeira solución para solucionar un problema é plantexar cal é o problema, non?
Pois iso foi o que fixemos na clase. Plantexar tódolos problemas.
EXERCICIOS:
Plantexamos os problemas dende o exercicio 22 ó 33 dos exercicios da parte de Repaso da ficha que nos deu a profesora Aia. A continuación poreivos algúns exemplos dos plantexamentos dos distintos tipos de exercicios.
Comezamos polo principio: Exercicio 22. Que di así:
22. Un test ten 40 preguntas. Por cada acerto obtéñense 2 puntos e por cada erro réstanse 0'5 puntos. Javier contestou tódalas preguntas e así obteu 45 puntos. ¿Cántas preguntas contestou correctamente?
Vale, despois de ler o enunciado vamos a darlle nomes a "x" e a "y":
X -> Nº de acertos.
Y -> Nº de erros.
O máis doado é a primeira ecuación, xa que o total de preguntas é 40, contando todas (acertadas e erradas):
 x + y = 40
x + y = 40Agora fixarémonos nos puntos que vale cada pregunta acertada e cada pregunta errada e os puntos totais que levou Javier:
2x - 0'5y = 45
E xa temos as dúas ecuacións plantexadas.
-----------------------
Ben, agora pasemos ó seguinte exemplo. O exercicio 25, que di así:
25. Un ciclista que vai a 25km/h persegue a outro ciclista que vai a 22km/h e que lle cheva unha ventaxa de 750m. ¿Cánto tempo tardará en alcanzao e qué distancia recorrerá hasta entón?

Primeiro facemos un debuxo cos datos para axudarnos a entendelo mellor.
t= tempo
Agora plantexaremos a ecuación que se refiere ó primer ciclista:
25= x + 0'75
t
25t = x + 0'75
Agora o ciclista 2:
22 = x
t
Se despexamos t nas dúas ecuacións podemos resolvelo por igualación:
 t= x + 0'75
t= x + 0'7525
t = x
22
E quedaría algo así:
x + 0'75 = x
25 22
--------------
E estes son algúns dos exemplos de tódolos exercicios que correximos na clase.
domingo, 24 de xaneiro de 2016
plantear problemas
Hoxe na clase de matemáticas aprendimos a plantear problemas nos que dous coches saen á vez un dende o punto A e o outro dende o punto B.
Un sae a unha velocidad e o outro a outra diferente. Para plantealo necesitamos a formula da velocidade.
Despois disto temos que pensar que xa se encontraron polo que deducimos o seguinte:
A partir de aí so queda resolver a ecuación.
martes, 19 de xaneiro de 2016
Corrección de exercicios.
18 de xaneiro de 2016.
Durante a clase de hoxe corriximos os exercicios 11 e 14, nos cales a profesora tivo que volver a explicar como se facían os sistemas de ecuacións con tres incógnitas que consiste en:
 Buscar una ecuación na cal una das incógnitas sexa un para colocala primeiro para mediante o método de reducción haxar a segunda ecuación e a terceira. É importante colocar enriba das flechas o paso que estamos facendo. Despexamos mediante o método de reducción ata ter nunha das ecuación unha única incógnita para atopar as solucións das ecuación restantes.
Buscar una ecuación na cal una das incógnitas sexa un para colocala primeiro para mediante o método de reducción haxar a segunda ecuación e a terceira. É importante colocar enriba das flechas o paso que estamos facendo. Despexamos mediante o método de reducción ata ter nunha das ecuación unha única incógnita para atopar as solucións das ecuación restantes.
Como por exemplo o apartado a do exercicio número 11.
Emma Tello Sánchez.
xoves, 14 de xaneiro de 2016
MÉTODO DE REDUCIÓN (GAUSS)
Xoves, 14 de Xaneiro 2016
Na clase de hoxe, aparte de correxir os exercicios do día anterior, aprendimos un novo método para resolver os sistemas de ecuacións: O método de redución (Gauss)
- Método de Gauss:
(E2) 2x-5y-2z= 5
(E3) 4x+7y+3z= 6
3. Unha vez que sabemos iso, utilizamos o método de redución co a primeira e segunda ecuación. Unha vez calculada a segunnda ecuación, Calculamos do mesmo modo a terceira.
4. Unha vez calculado todo solo temos que despexar a "x", a "y" e a "z" para saber a que equivalen.
Audio explicativo do voki:
Video explicativo:
Páxinas explicativas: http://www.vadenumeros.es/primero/sistemas-gauss.htm
http://www.vitutor.com/ecuaciones/2/gauss.html
http://profesor10demates.blogspot.com.es/2013/10/sistemas-de-ecuaciones-lineales-por.html
martes, 12 de xaneiro de 2016
Luns, 11 de xaneiro do 2016
Hoxe na clase non fixemos nada mais que correxir os exercicios que a profesora Aia nos mandara facer de sistemas de ecuaciones. E para todos aqueles que ainda non vos saian deixovos un vídeo explicatorio:
venres, 8 de xaneiro de 2016
División de polinomios
E para continuar, por se queredes repasar o que vimos hoxe, ou para que poidades entendelo os que non viñestes á clase, déixovos un vídeo no que se explica a división de polinomios. Empezade a visualización no minuto 4.
Xa me diredes o que vos pareceu.
Xa me diredes o que vos pareceu.
Tema 4: Polinomios
Chega o novo trimestre e comezamos con... ÁLXEBRA:
Non, non é para tanto. Como xa dixen na clase, en realidade, acostuma a ser a parte do temario que menos vos custa. Para comezar, varios vídeos para repasar os contidos que xa coñecedes dos cursos pasados:
Definicións básicas
Valor numérico dun polinomio
Suma de polinomios
Resta de polinomios
Multiplicación de polinomios
Non, non é para tanto. Como xa dixen na clase, en realidade, acostuma a ser a parte do temario que menos vos custa. Para comezar, varios vídeos para repasar os contidos que xa coñecedes dos cursos pasados:
Definicións básicas
Valor numérico dun polinomio
Suma de polinomios
Resta de polinomios
Multiplicación de polinomios
xoves, 7 de xaneiro de 2016
2ª AVALIACIÓN
Sistemas de ecuacións
Substitución:
- Despexas a x ou a y nunha das ecuacións.
- Substitúes o anteriormente despexado na outra ecuación.
- Resolves a ecuación.
- Co resultado averiguas o valor do primeiramente despexado substituíndo ese valor pola letra correspondente.
Igualación:
- Despexas x ou y nas dúas ecuacións.
- Igualas os dous resultados e resoves dita ecuación.
- Elixes un dos dous despexes e substitúes o resultado da outra ecuación pola letra correspondente.
Redución:
- Multiplicamos nunha ou nas dúas ecuacións por un número calquera para obter o mesmo número na x ou na y pero un positivo e outro negativo, para así poder eliminalo e sacar unha incógnita da ecuación.
- Resolvemos a ecuación resultante e subtituimos o resultado nunha das ecuacións iniciais.
Dobre redución:
- facemos o mesmo que na anterior opción pero antes de substituir o valor volvemos a reducir as ecuacións pero eliminando a outra incógnita.
Resolución gráfica:
- Despexas a x ou a y nas dúas ecuacións.
- Fas unha tabla e vas probando números que den exactos ao substituilos nas ecuacións e creas a tabla das x e y con dous valores en cada columna.
- Debuxas unha gráfica e colocas os valores nela cunha recta diferente para cada ecuación.
- Se as dúas rectas se cruzan, o punto no que se cruzan é o resultado, se pasan xusta unha por encima da outra significa que ten infinitas solucións e se non se cruzan en ningún lado é que non ten solución.
Subscribirse a:
Comentarios (Atom)